この記事には広告を含む場合があります。
記事内で紹介する商品の購入やアプリをダウンロードすることで、当サイトに売り上げの一部が還元されることがあります。
「フェルマーの最終定理」
歴史上もっとも難しい証明と言われ300年以上天才数学者たちの挑戦を阻んできた難攻不落の問題。曰く、悪魔でも解くことができない。
この数学界最強の難問を世界、そして日本の数学者も巻き込んで完全証明するまでの軌跡をサイモン・シンが描いたノン・フィクションが書籍『フェルマーの最終定理』です。
数学を題材にした書籍ですが、これは歴史的な難問に挑んだ数学者たちのドキュメンタリーだ。歴代の数学者たちの熱い戦いはまるで歴史小説や企業小説を読んでいるようなドラマに満ちた物語になっており文系のあなたでも(私もですが)まず間違いなく感動できる傑作になっています。
 ガチで面白い小説おすすめ小説2025!読み始めたら止まらない名作を厳選紹介
ガチで面白い小説おすすめ小説2025!読み始めたら止まらない名作を厳選紹介
『フェルマーの最終定理』とは
フェルマーの最終定理 / 著者:サイモン・シン、訳:青木薫
17世紀、ひとりの数学者が謎に満ちた言葉を残した。「私はこの命題の真に驚くべき証明をもっているが、余白が狭すぎるのでここに記すことはできない」以後、あまりにも有名になったこの数学界最大の超難問「フェルマーの最終定理」への挑戦が始まったが――。天才数学者ワイルズの完全証明に至る波乱のドラマを軸に、3世紀に及ぶ数学者たちの苦闘を描く、感動の数学ノンフィクション!
裁判官であり余暇に数学を嗜んでいたというフェルマー。彼が古代ギリシャの数学者ディオファントスが著した『算術』に注釈をつけたもの(メモのようなもの)を死後に長男サミュエルが再出版したことがこの謎の始まりである。
彼が残した48の命題のうち47の命題は後の数学者の手によって解かれたがどうしても一つ解けない問題があった。それがフェルマーの残した最後の定理、つまり「フェルマーの最終定理」である。
『フェルマーの最終定理』を読んだ感想
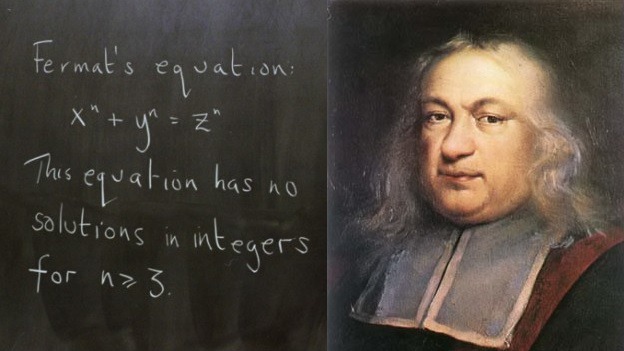
そもそも「フェルマーの最終定理」とはどんな問題なのか?
「フェルマーの最終定理」という言葉を聞いたことがあってもどんな問題なのか実際に知っている人は少ないのではないでしょうか?300年間天才数学者の挑戦を阻んだ、悪魔でも解けない問題ですからね。途方もなく複雑な数式を想像してしまいますよね。
私も本書でその問題を初めて目にしたんですが唖然としました。「フェルマーの最終定理」とはこんなにもシンプルな問いなのかと。
「方程式 xn+yn=zn が n>2 の場合、 x,y,zは0でない自然数の解を持たない」
え?こんなにシンプルな数式なの?正直あっけにとられました。
しかし、このシンプルな問題が多くの数学者を狂わせていくことになるのです。
フェルマーの最終定理は正確には「定理」ではなかった

先の方程式「方程式 xn+yn=zn が n>2 の場合、 x,y,zは0でない自然数の解を持たない」に対して適当な数字を入れていくとフェルマーのいうように解がありません。思いつく限りの自然数を入れてみても解がありませんので一見するとフェルマーのいってることは正しく見えます。
では、なぜ多くの数学者がこれに悩んでいたかと言うとこの方程式を「証明」できなかったからです。定理とは完璧に証明されて「真」であることが分かってはじめて「定理」になります。
つまり、本来は証明されるまでは「定理」ではなく「予想」として扱うべき問題でした。「フェルマーの最終予想」と実際に呼ばれることもありました。
なぜ証明できなかったのか?無限という概念

ではなぜこんな簡単そうに見える数式で、あらゆる数字を入れても成り立つものが証明できなかったのでしょうか?その答えは「無限」です。
「無限」とは文字通り限りが無いこと…
つまり、一見するとどんな数字を当てはめても成り立つ「フェルマーの最終定理」も無限の彼方にある数字の組み合わせ次第では成り立たないかもしれない。この無限の彼方にある我々では想像できないようなどんな自然数の組み合わせでも成り立たないとどうして断言できるのか?ということがどうしても証明できなかったんです。
このシンプルな方程式の証明は「無限の自然数の組み合わせ」でも成り立つをことを証明しないといけない途方もない挑戦だったのです。
この数式の証明はまずは具体的な数字を証明することで始まりました。n=4のとき、n=3のとき…という具合です。この流れをジェルマン、クンマーという数学者が飛躍させましたが完全証明とはいきませんでした。
日本の天才数学者の「予想」がフェルマーの最終定理に大きくかかわってくる
時は大きく流れ戦後の日本。野心的な日本の数学者谷山豊と志村吾郎が「すべての楕円曲線はモジュラーである」という大胆な予想を打ち立てます。この「谷村-志村予想」こそがフェルマーの最終定理を解く大きなカギになっていきます。
この「谷村-志村予想」、はじめはあまり注目されていなかったんですがフライという数学者の予想により超重要な予想へと進化するんですよね。
曰く、
フェルマーの最終定理に対する反例 an + bn = cn からはモジュラーでない楕円曲線(フライ曲線):y2 = x(x − an)(x + bn)
が得られ、これは谷山–志村予想に対する反例を与えることになるというアイディアを提示
なんのことかわかんないですよね。これは背理法と言う証明方法で
- フェルマー予想が偽である(フェルマー方程式が自然数解をもつ)と仮定
- この自然数解からは、モジュラーでない楕円曲線を作ることができる。
- しかし、「谷山・志村予想」が正しいならば、モジュラーでない楕円曲線は存在しない
- 矛盾が導かれたので仮定が誤っている
- よってフェルマー予想は真である
ということを言ってるんです。もちろん、この時点ではフェルマーの最終定理は証明されていません。しかし、「谷村-志村予想」が証明できれば「フェルマーの最終定理」を証明したことになる、ということを示してるんです。
どうです?テンション上がりませんか?私はこの部分を読んでいて「うぉおおお!」ってなりました。日本の若き数学者の研究がフェルマーの最終定理に繋がっていたのかと思うと感動して涙が出てきそうになります。
そして、アンドリュー・ワイルズがそのアイディアに触れついに「フェルマーの最終定理」に挑むことになるのです。
ワイルズがどのようにこの難問を解くのか。どんなドラマが待ち受けているのか。続きは自身の目で確かめてください。
美しい数学の世界
さて、本書を読んでいると「フェルマーの最終定理」だけではなく数学者たちが解き明かしてきた「美しい数学」の断片を目の当たりにすることができます。
私たちが学生時代に倣った数々の数学、公式などその最たるもので偉大な数学者たちが血反吐をはくような研鑽の果てに証明した「真理」だということをいまさらながらに思い知らされました。
これが本当におもしろい。インド人が0を発明したというのはあまりにも有名ですが、数学の世界が広がっていく過程が恐ろしく美しい。まずは自然数が積みあがっていく。3を5で割ったら自然数で表すことができないから分数ができる。3から5を引いたら自然数では対応できなくなりマイナスの世界が生まれる…素数、無理数、虚数…などなど。
問題にぶつかったら予想を立て、証明し、定理にする。そうやって広がった数学の世界はまさに美しいと言えるでしょう。是非その感動を味わってほしいです。
フェルマーの最終定理、残された謎
天才数学者のワイルズの手によって証明された「フェルマーの最終定理」。それは、谷村-志村予想だけでなく現代数学の粋を集めて解いた英知の結晶です。
となると、ひとつ疑問が出てきますよね。
「私はこの命題の真に驚くべき証明をもっているが、余白が狭すぎるのでここに記すことはできない」
と言う謎めいた文章を残したフェルマー。このフェルマーは300年以上前にどうやってこの難問を証明したのか?17世紀の数学の知識で解かれた証明方法は今なお明らかになっていません。もしかしたらフェルマー自身解けていない可能性すらあるのです。
証明されてもなお残る大きなロマン。これこそが「フェルマーの最終定理」の魅力なのです。





